2021-06-11 08:47:48 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源:河南分院
沈北华图为您提供最新的备考文章:2022年辽宁省考行测之工程问题,快人一步。更多招聘信息及备考文章敬请关注辽宁沈北华图网站(http://shenbei.huatu.com/)或关注辽宁沈北华图微信公众号(shenbeiht),辽宁沈北华图咨询电话:024-89747699。
2021年对我们每个公民来说都是不平凡的一年,经历过疫情的冲击,各行各业都面临着工作难的问题。在这样一个大背景下,我们公务员却增大了招生量,这对于我们来说是一次莫大的机会。那我们何不借助此次扩招的机会,逼自己一把,让自己成为一名优秀的人民公仆呢?那么,我们今天就来聊聊公考行测数量关系模块中相对比较简单的一个题型:工程问题。
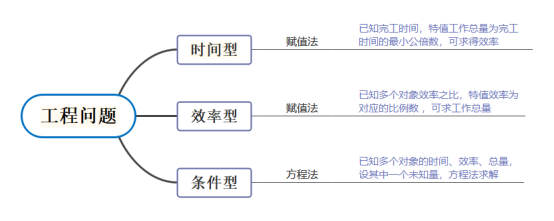
历年公考,工程问题几乎是必考题型,并且也是一个在考场上能够快速拿分增强考生自信心的题型。一般来说,工程问题常考的有三种题型:时间类、效率类、条件类,常用的解题方法有赋值法和方程法两种。
时间类
时间类的工程问题一般给的条件都是某人或者某个队伍完成某项工程的时间,一般用赋值法来解题,赋工程的工作总量为题干中给定完成时间的公倍数。
【例1】一项工程,甲一人做完需30天,甲、乙合作完成需18天,乙、丙合作完成需15天,甲、乙、丙三人共同完成该工程需:( )
A.10天 B.12天
C.8天 D.9天
适用前提剖析:
整个题干中给出的都是完成时间,是典型的时间类工程问题,用赋值法解题。
【解析】赋工作总量为90(30、18、15的公倍数),根据题意可知,甲的效率为3,甲乙的效率为5,乙丙的效率为6,则乙的效率为2,丙的效率为4,故甲乙丙的效率和为2+3+4=9,所以三人共同完成需90÷9=10(天),因此,选择A选项。
效率类
效率类工程问题一般在题目中会给定效率之间的关系,或者通过一步简单转化找到效率之间的关系,一般解题方法是赋值效率。
【例2】甲工程队与乙工程队效率之比为4:5,一项工程由甲队单独做6天,再由乙队单独做8天,最后由甲乙两个工程队合作4天刚好完成,如果这项工程由甲工程队或乙工程队单独完成,则甲工程队所需天数比乙工程队所需天数多多少天:( )
A.9 B.4
C.5 D.6
适用前提剖析:
题干中给出两人效率之间的关系,符合效率类工程问题,可赋值效率,再结合给定的相关时间条件解题。
【解析】赋值甲乙的效率分别为4、5,根据题意可知,甲单独完成工作量为4×6=24,乙单独完成的工作量为5×8=40,二者合作完成的工作量为(4+5)×4=36共完成24+40+36=100,则总做总量即为100,故甲单独完成所需要的时间为100÷4=25天,乙单独完成所需要的时间为100÷5=20天,所以甲单独完成所需天数比乙多25-20=5天。因此,选择C选项。
条件类
条件类工程问题一般给的条件比较多,时间、效率、总量中至少给定其中两类量,一般用方程法解题。
【例3】甲乙两个工程队共同修建一段长为2100千米的公路,甲队每天比乙队少修50千米,甲队先单独修3天,余下的路程与乙队合修6天完成,则乙队每天所修公路的长度是:
A. 135千米 B. 140千米
C. 160千米 D. 170千米
适用前提剖析:
1、整个题干中给出的具体数据,包含时间、总量以及甲乙效率之间的关系。
2、总量、时间、效率三类量都涉及到,是条件类工程问题,用方程法解题。
【解析】设乙队每天所修长度为x,则甲每天修x-50,根据题意可列式子3(x-50)+6(x+x-50)=2100,得x=170(千米)。因此,选择D选项。
通过上面几个例题,相信大家已经掌握了工程问题常见的三大题型,希望大家在自己的备考过程中能熟练应用这三种工程问题的解题技巧,相信在考场上碰到类似题目,定能如鱼得水,快人一步。
(编辑:沈北华图02)

贴心微信客服

贴心QQ客服
上一篇: 2021年沈阳工程学院招聘工作人员(第二批)取消部分岗位公告
下一篇:没有了